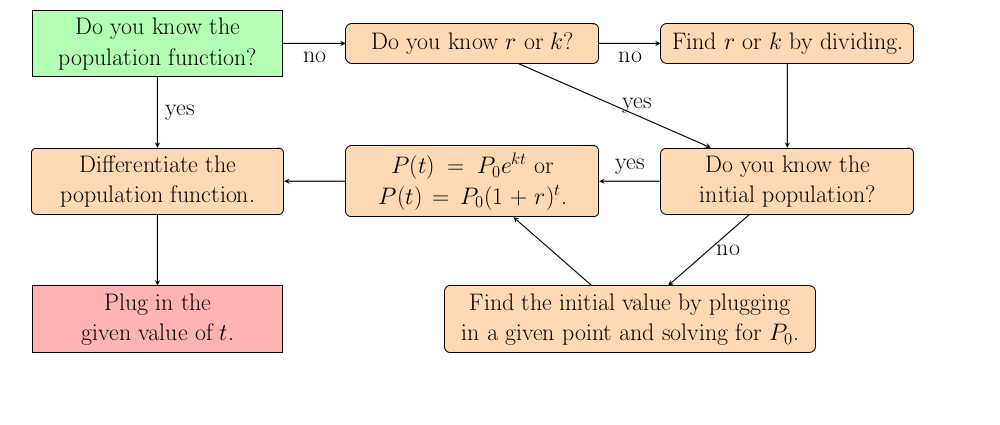
How do I calculate how quickly a population is growing?
A population grows exponentially and you are asked to determine how fast the population is growing at a certain point in time. Growth really means change and change is code for take the derivative. Take the derivative of the population function and evaluate at the given time.What if the population function is not given?
The above step is usually all the Calculus required and since the functions are often exponential the derivative is not too hard. To make a question more difficult you may not be given the population function but still asked to find the rate of growth function. The first step in this case is to find the population function.
How to find the population function is going to depend on what information is given to you. You are going to need to find the initial value of the population and the rate at which it grows. If you know the population at two different times you can plug in these two points and determine the rate. Then you can find the initial value by using one point and the rate to solve for $P_0$. Then just plug everything into the appropriate formula.
How do I calculate when a population is growing at a certain speed?
Sometimes a question will ask when a population is growing at a rate of $10$ feet per second or some other value. The process begins the same way by taking the derivative of the population function. But if you are not given a time then you cannot simply plug into this derivative.
Instead you must solve for the time. You can compute the growth at any time, and you want to know at what time the growth is a certain speed. Thus you will set the derivative equal to the given speed and solve for $t$. Because $t$ is likely in the exponent you will probably need to take a natural logarithm to solve, but if you remember your properties of logarithms then this should be easy enough.

