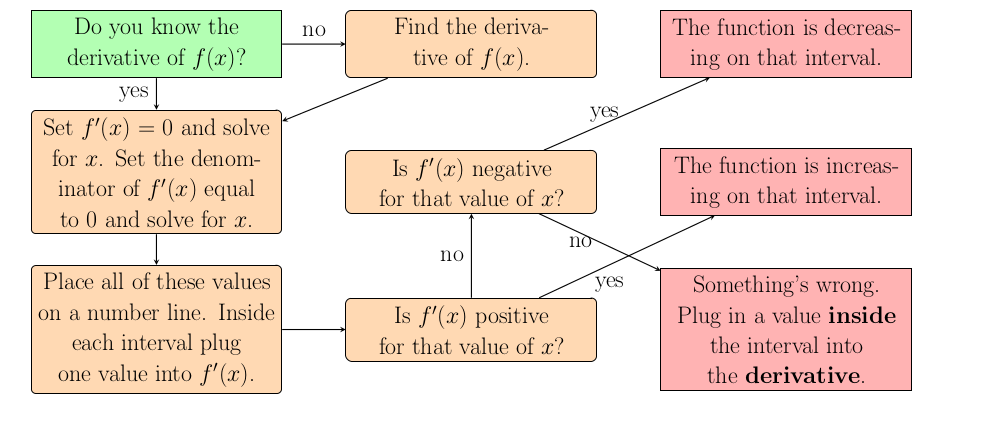
When is a function increasing?
A function is considered increasing on an interval whenever
the derivative is positive over that interval. And the function is decreasing on any interval in which the derivative is negative.
How do we determine the intervals?
The first step is to
take the derivative of the function. Then solve for any points where the derivative equals 0. That is, solve for all $x$ such that $f'(x)=0$. Then we need to find any points where the derivative is undefined, so we set the denominator of $f'(x)$ equal to 0 and solve for all such values of $x$. These values of $x$ will form the endpoints of potential intervals.
How do we know if the function is increasing on an interval?
Once the intervals are established we must determine whether the derivative is positive or negative on each interval. The simplest thing to do is to plug in any value in that interval into the derivative and see if the output is positive or negative. Any value on an interval should have the same sign so choose the value that is easiest to plug in. You don't have to actually find the derivative just figure out if it is positive or negative. Be careful to plug into the derivative and not the original function.


