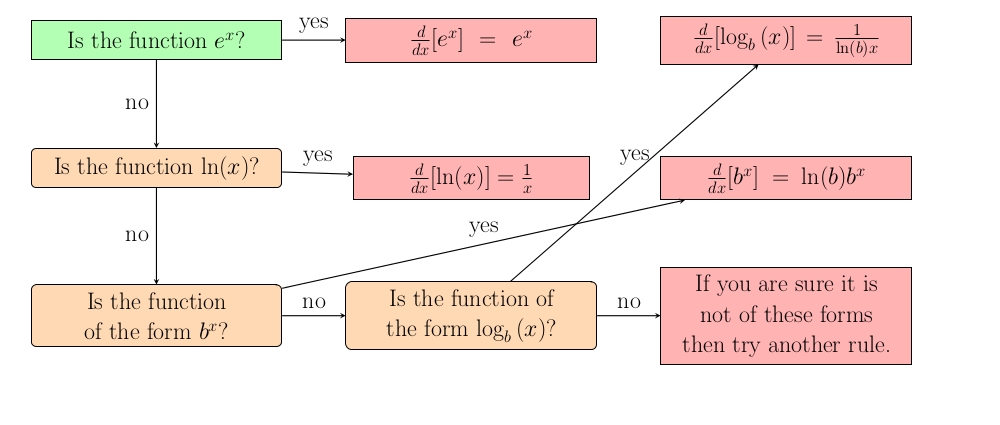
What is the derivative of an exponential or logarithmic function?
The most common functions in this category are $e^x$ and $\ln(x)$. So you definitely need to learn that the derivative of $e^x$ is $e^x$ and the derivative of $\ln(x)$ is $1/x$. Although base $e$ may seem confusing, these functions are most common in Calculus class because they are the easiest to differentiate. Other bases have similar derivatives, but they involve ugly constant terms.
When can we treat the function as an exponential?
Is the function of the form $b^x$ where $b$ does not depend on $x$? If so, then we can treat the function as an exponential. This base could be $e$ (and often is), a positive integer, a fraction, or some other constant. The only real confusion could arise if the function looks like $\frac{1}{4^x}$ or $4^{-x}$ or $(1/2)^{2x}$. These are all the same function, but in order to treat the function as an exponential you must rewrite them to $(1/4)^x$. The exponent must exactly be $x$. We will learn other methods to deal with non-$x$ exponents later, but using properties of exponents allow for an easy method to make the function more basic.
How do we differentiate an exponential function?
Determine the base of the exponential. Take the natural logarithm of this base. Multiply this natural logarithm by the original function. If the base is $e$ then the natural logarithm of $e$ is 1 so the $\ln(e)$ can be ignored. If the base is an integer, like 2, then usually you just want to leave the natural logarithm in your answer, like $\ln(2)2^x$, rather than approximating.
When can we treat the function as a logarithmic function?
Is the function of the form $\ln(x)$ or $\log_b(x)$? If not, you need to be able to rewrite the function using properties of logarithms so that the inside of the logarithm is simply $x$.
How do we differentiate a logarithmic function?
Determine the base of the logarithm. Take the natural logarithm of this base. Multiply this natural logarithm by $x$ and place that product in the denominator of a fraction with a numerator of 1. Again, if the base is $e$ the natural logarithm does not change the expression. And if the base is an integer leave the natural logarithm in your answer.


