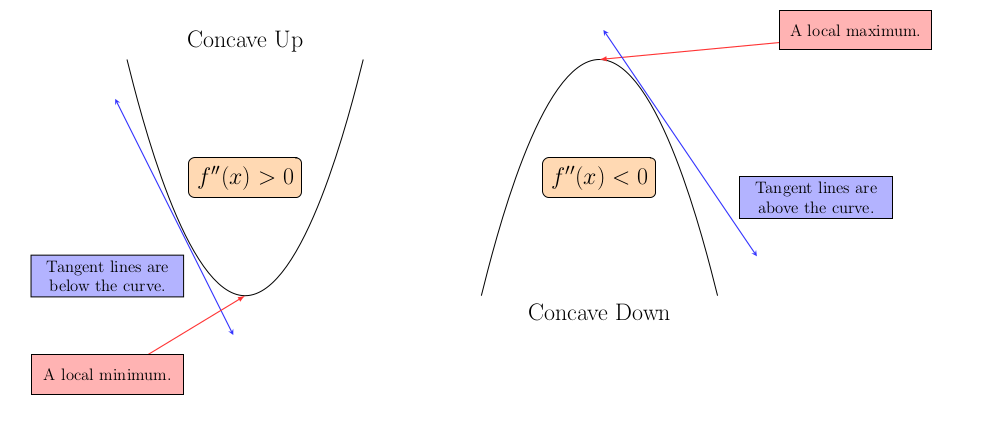
When is a function concave up?
When the second derivative of a function is positive then the function is considered concave up. And the function is concave down on any interval where the second derivative is negative.
How do we determine the intervals?
First, find the
second derivative. Then solve for any points where the second derivative is 0. That is, find all $x$ such that $f''(x)=0$. We also need to consider any values that make the second derivative undefined, so if there is a denominator check when it is 0 and add any of these values to our list. These values will be the possible endpoints of the intervals we want to consider.
Which intervals are concave up?
Inside each interval the second derivative is either positive or negative for the entire interval since we know it does not cross 0 within the interval. Therefore we just need to check whether the second derivative is positive or negative for one value from each interval. So pick the value inside each interval that is easiest to plug in and determine if the second derivative is positive or negative. If it is positive then the function is concave up on that interval, and if the second derivative is negative then the function is concave down on that interval. Just be careful to plug into the correct function. Use the second derivative not the first derivative or the original function.


