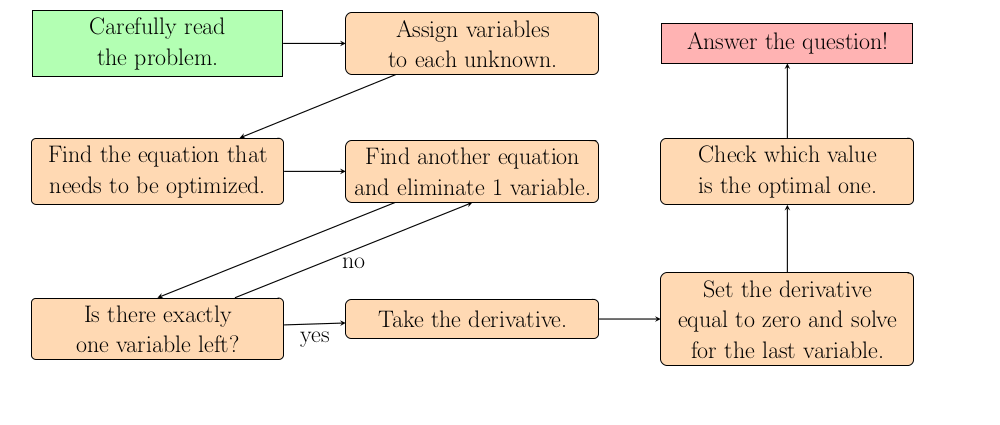
Where do I begin?
From the problem write down as much information as possible. Define variables for any unknowns. Write down relevant equations. Determine what you need to optimize. You can always add more information as needed, but start by at least writing down something you know and something you need to find out.What is my first goal?
Every optimization word problem will end the same way. You want to create one equation that involves one variable so that you can differentiate and solve.
This might be simple if there is only one equation and one unknown. If you have more than one unknown then you will need to eliminate all but one variable with additional equations or formulas. Some equations may be given in the problem while others will require previous knowledge (generally simple geometric formulas like the area of a triangle). These equations are generally called constraints and involve at least two of your variables.
How do I eliminate variables?
Determine the equation that you need to optimize. The problem should have some final question. Turn this question into an equation using as many variables as necessary. If the question asks for the maximum area then create an equation to determine the area even if the equation depends on two or more variables. If the question asks for the minimum cost then create an equation for the cost.
Now if there is more than one variable you will need to find an equation that relates two or more variables in this equation. Generally the problem provides some sort of constraint like the sum of the height and length is less than some value. If the problem talks about perimeter you need to know that can used to create an equation with heights and lengths. Carefully read the problem to identify some information about what constraints there are on the variables.
Turn this information into an equation and solve that equation for one of the variables. In the equation you need to optimize, replace that variable with the equation in terms of another variable. Now the equation should depend on one fewer variable. Repeat this process until exactly one variable remains.

