What is the derivative of a function?
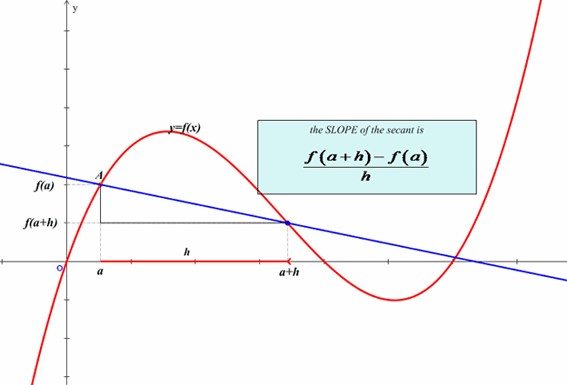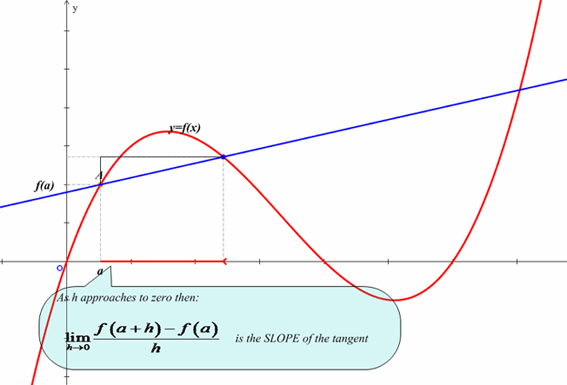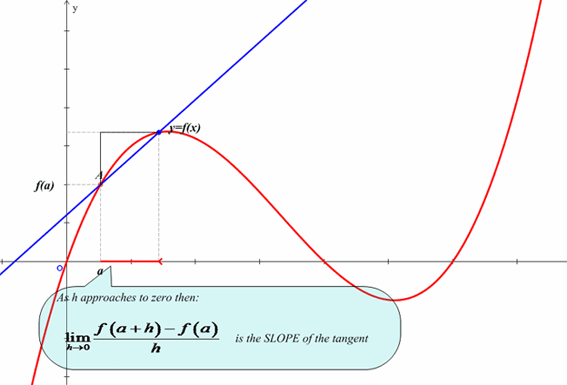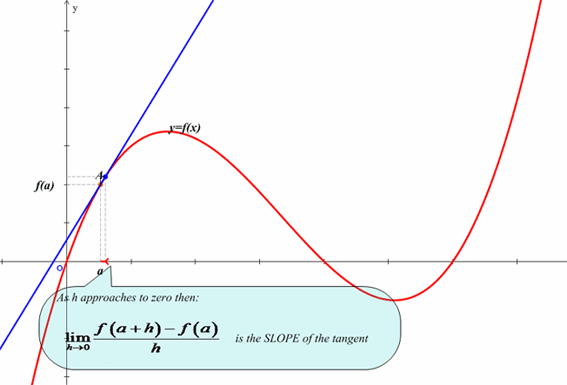
The derivative is a function that outputs the instantaneous rate of change of the original function. Instanstaneous means analyzing what happens when there is zero change in the input so we must take a limit to avoid dividing by zero. Fortunately mathematicians have developed many rules for differentiation that allow us to take derivatives without repeatedly computing limits. However, remembering that the derivative is a limit is often beneficial, especially when applying the derivative to solve word problems.What do all these symbols mean?
There are two popular ways to denote the derivative of a function: $f'(x)$ and $\frac{d}{dx}[f(x)]$. Each notation has advantages and can be used when most appropriate. The notation $f'(x)$ is short and to the point which is why this form is seen often in most Calculus courses. However, there are two main disadvantages.
With $f'(x)$ the variable of differentation is not always clear and the function must be defined separately. In order to ask for the derivative of something like $x^2$ you must first define that $f(x)=x^2$ rather than simply asking for $\frac{d}{dx}[x^2]$. And remember that differentation is always taken with respect to some variable, usually but not always $x$, and $f'(x)$ does not always make it clear what this variable is. What is $f'(3)$? Answering this question requires knowing $f$ and knowing the independent variable of $f$. Of course, there is not a nice way of asking for $f'(3)$ in $\frac{d}{dx}$ notation.
The notation $\frac{dy}{dx}$ stands for the derivative of $y$ with respect to $x$. And $\frac{d}{dx}[f(x)]$ stands for the derivative of $f(x)$ (or whatever function is inside the brackets) with respect to $x$. This notation is often used to ask for a derivative without defining extra functions or when the variable of differentiation is an important part of the question.
Do not be scared away by either notation. Understanding the notation may seem unneccessary, but very few students succeed at Calculus without learning what a derivative really is and what the notation means.

