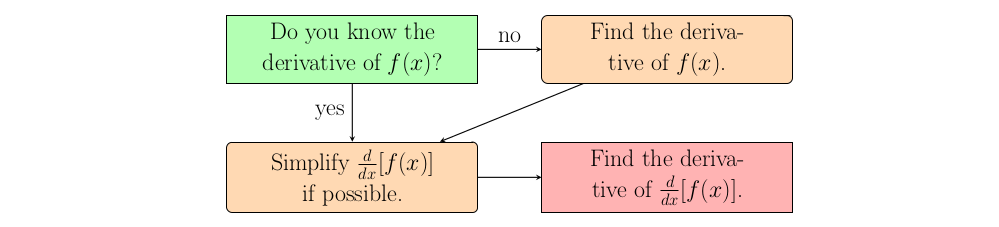
How do we take the second derivative?
Assuming you know how to take the first derivative, the second derivative really is not anything new. Take the derivative as you normally do. Then you may wish to simplify this derivative if possible to make the next step easier. Finally, take the derivative of the derivative in the same way as you would any other function. Now you have the second derivative.Why do we take the second derivative?
The second derivative identifies the concavity of the function. Concavity determines whether a function is at a maximum or minimum. As we will see later, the second derivative gives the acceleration of a function. Also, second and higher power derivatives are important in Taylor series in future Calculus classes.What about third derivatives and beyond?
Derivatives beyond the second derivative do have applications and are no more complicated. The third derivative, as expected, is found by taking the derivative of the second derivative. In general there is no way to find these derivatives without differentiating the full series of derivatives.
However, some functions have very predictable patterns for multiple derivatives. The easiest case is the exponential function. What is the $12^{th}$ derivative of $e^x$? The second derivative is $e^x$ so the third derivative is as well and this pattern continues forever so the $12^{th}$ derivative is the same as the first and thousandth derivatives.
What about trigonometric functions? Take a few derivatives of $\sin(x)$ and try to identify the pattern. Since the derivatives of sine and cosine swap with an extra negative, any further derivative will either be $\pm\sin(x)$ or $\pm\cos(x)$ and you should work out when it is each of these.
For power functions, the exponent will decrease by one each time until the derivative becomes $0$ at which point any further derivative will also be $0$. Can you develop a formula for the coefficient of the $k^{th}$ derivative of $x^n$?
Can I get one example?
The second derivative is only harder than the first derivative because it requires two derivatives and the derivative function will likely be at least a little complicated.
A relatively simple example is to take the second derivative of $x\ln(x)$. The first derivative is $\ln(x)+1$ from the product rule. Then the second derivative is $\frac{1}{x}$ since we know the derivatives of $\ln(x)$ and $1$.

