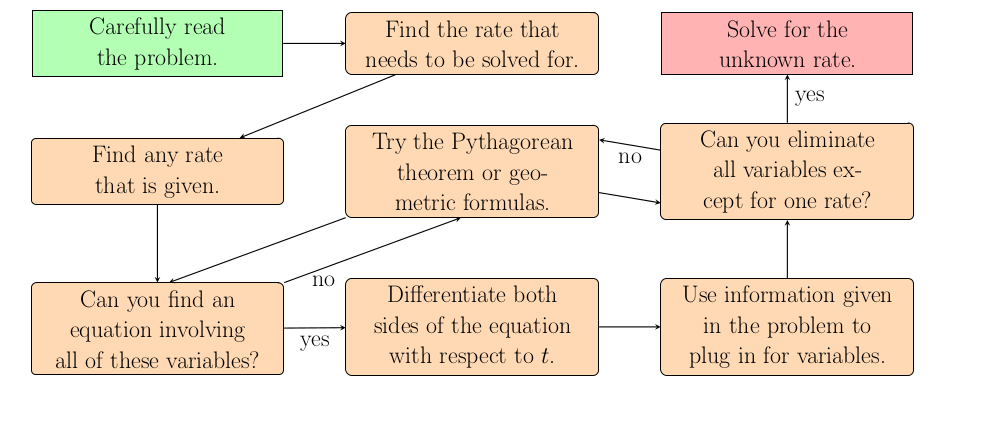
Where do I begin?
Read the problem and find a rate that is given. Write this rate in a form similar to $\frac{dX}{dt}=R$ where $X$ is the variable that is changing and $R$ is the rate at which it is changing. Units are important, especially if multiple different scales are used, so make sure to include these in your equation. For instance, if the volume is increasing at a rate of $5$ feet per second then write down $\frac{dV}{dt}=5\frac{f}{s}$.What do I do next?
Read the problem and find the rate that you are asked to solve for. Write this rate in a form similar to $\frac{dX}{dt}$ where $X$ is the variable that is changing at an unknown rate. For instance, if the question asks how fast the radius is increasing then note that you want to solve for $\frac{dr}{dt}$.How do I use what I know to get what I want?
We need to use the rate we know to determine the rate we are asked to find. So we need an equation that relates these two rates. Since rates are derivatives of functions what we need first is an equation that relates the two variables. We need to find an equation that involves the variable whose rate of change we know and the variable whose rate of change we want to know. For instance, if the question gives us the rate of change of the volume of a sphere and asks for the rate of change of the radius then we want an equation that involves $V$ and $r$.
Sometimes this equation will be somehow provided in the problem, but often we will need to know some geometric formula. Know the formulas for area and volume of basic shapes as well as the Pythagorean theorem. The volume of a sphere is $V=\frac{4}{3}\pi r^3$, and this formula allows us to convert a rate involving volume to one involving radius or vice versa.
How do I solve for the rate?
Once you have the proper equation then you want to differentiate this equation with respect to time. You may have to use implicit differentiation, so make sure you differentiate both sides of the equation. Although $t$ will likely not appear in the equation, your variables are functions of $t$ so the chain rule applies and both rates should appear after differentiating.
After differentiating you should be able to plug in every value you know and there will only be one unknown left. Solve for this rate and you are done. For instance, differentiating $V=\frac{4}{3}\pi r^3$ yields $\frac{dV}{dt}=3\frac{4}{3}\pi r^2\frac{dr}{dt}$. Then plug in the known rate of change of volume. At this point the only unknown left other than $\frac{dr}{dt}$ is $r$, and you should be able to figure this out from the problem. The question should mention something about when to compute the rate of change. If the problem is meant to be easy then the radius will be given directly. If the problem is meant to be harder then you might be given the diamter or the volume of the sphere. Compute the radius from this information. Often you will reuse the equation that was differentiated to solve for the final variable.
Once the only unknown that remains is the rate you want to find then you can solve for that rate. Likely the equation will be a simple linear function of the rate so just divide by everything else. If the problems involves more than two rates, the process is the same but you will need to be given more information to plug in.

