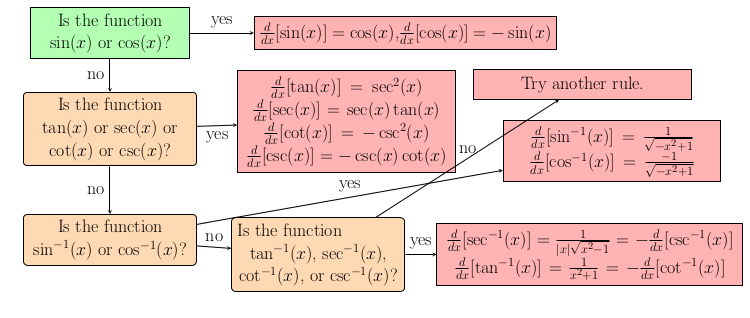
When do we apply trig differentiation?
The function must be exactly of the form $\sin(x)$ or another trig or inverse trig function evaluated at $x$. There cannot be anything else inside the parentheses and the outside must simply be the trigonometric function. Other rules like the
chain rule or
product rule will be required if the function is more complicated.
How do we differentiate a trig function?
There are twelve possible functions and you probably want to memorize each of their derivatives. If you learn the derivatives of sine and cosine then you can apply the quotient rule to determine the other four derivatives. However, most students just memorize these derivatives to save time and work on exams since there are a limited number of functions to learn. The table below lists the derivatives. If a function looks exactly like the function in the left column, then its derivative is found in the right column.
What are the derivatives of the trig functions?
| $f(x)$ | $\frac{d}{dx}[f(x)]$ |
|---|
| $\sin{(x)}$ | $\cos{(x)}$ |
| $\cos{(x)}$ | $-\sin{(x)}$ |
| $\tan{(x)}$ | $\sec^2{(x)}$ |
| $\cot{(x)}$ | $-\csc^2{(x)}$ |
| $\sec{(x)}$ | $\sec{(x)}\tan{(x)}$ |
| $\csc{(x)}$ | $-\csc{(x)}\cot{(x)}$ |
| $f(x)$ | $\frac{d}{dx}[f(x)]$ |
|---|
| $\sin^{-1}{(x)}$ | $\frac{1}{\sqrt{-x^2+1}}$ |
| $\cos^{-1}{(x)}$ | $\frac{-1}{\sqrt{-x^2+1}}$ |
| $\tan^{-1}{(x)}$ | $\frac{1}{x^2+1}$ |
| $\cot^{-1}{(x)}$ | $\frac{-1}{x^2+1}$ |
| $\sec^{-1}{(x)}$ | $\frac{1}{|x|\sqrt{x^2-1}}$ |
| $\csc^{-1}{(x)}$ | $\frac{-1}{|x|\sqrt{x^2-1}}$ |


