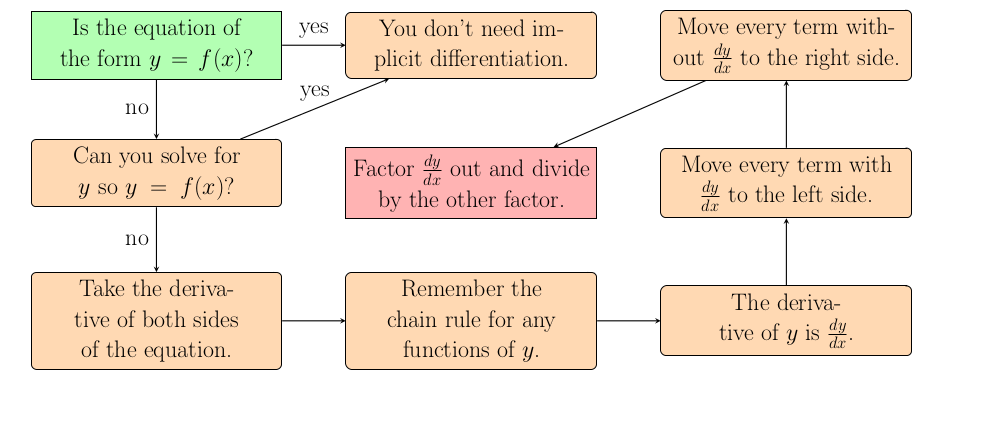
When do we use implicit differentiaion?
When an equation is not solved for $y$ then try to solve for $y$. However, if it is not possible to solve for $y$ and we are asked to find $\frac{dy}{dx}$ then it is time to use implicit differentiation. We will be able to find the derivative, but only at the cost of being slightly more involved. Normally we expect the derivative to be a function of $x$, but with implicit differentiation the derivative will be a function of both $x$ and $y$.How do we use implicit differentiation?
Take the derivative of both sides of the equation. Be careful whenever $y$ appears to treat it as a function of $x$ and correctly apply the chain rule. The expression $\frac{dy}{dx}$ will appear every time you differentiate $y$, and the next step is to solve for $\frac{dy}{dx}$. Collect all of the $\frac{dy}{dx}$ on one side and factor it out before dividing. Solving for $\frac{dy}{dx}$ should be easy since the equation will be linear with respect to $\frac{dy}{dx}$. Then you have the derivative you are seeking without ever knowing what $y$ actually is as a function of $x$. Although the function iwll depend on $x$ and $y$ so you will need to know both coordinates to compute the derivative at a particular point.Can I see an example?
Suppose $\sin(y)=x$ and we want to find $\frac{dy}{dx}$. One possibility for this problem is to solve for $y$ and then use the derivative of arcsine, which you should have memorized. However, we should get the same result if we do it implicitly.
Take the derivative of both sides. We can apply the chain rule with $y$ as the inside function and sine as the outside to get $\frac{d}{dx}[\sin(y)]=\cos(y)\frac{d}{dx}[y]=\cos(y)\frac{dy}{dx}$ and it should be obvious that $\frac{d}{dx}[x]=1$. Thus after differentiation we have $\cos(y)\frac{dy}{dx}=x$.
Solving for $\frac{dy}{dx}$ is easy since we just divide by $\cos(y)$ to yield $\frac{dy}{dx}=\frac{x}{\cos(y)}$. This derivative does not look like the derivative you memorized for arcsine, so what is the difference?
This derivative still depends on $y$, but we will try to replace $\cos(y)$ with a function of $x$. We are lucky with this example and can actually rewrite $\cos(y)$ as $\sqrt{1-x^2}$ since $\cos^2(y)+\sin^2(y)=1$ and we know what $\sin(y)$ is. Now using $\sqrt{1-x^2}$ as the denominator makes our answer look familiar. Although this example did not require implicit differentation it is always good to see that our new methods match what we expect from old methods.
One more example?
What if we make it a bit more complicated so that we cannot solve for $y$? Find $\frac{dy}{dx}$ when $y\sin(y)=x$. Now the derivative will have to depend on $y$.
Taking the derivative of both sides is again easy on the right side, but the left requires a product and chain rule so be careful. Using the product rule, $$\frac{d}{dx}[y\sin(y)]=y\frac{d}{dx}[\sin(y)]+\sin(y)\frac{d}{dx}[y].$$ We already found derivatives of $\sin(y)$ and $y$ so plug them in to get $$\frac{d}{dx}[y\sin(y)]=y\frac{d}{dx}[\sin(y)]+\sin(y)\frac{d}{dx}[y]=y\cos(y)\frac{dy}{dx}+\sin(y)\frac{dy}{dx}=\frac{dy}{dx}(y\cos(y)+\sin(y)).$$
The last thing we did was factor out the $\frac{dy}{dx}$ so that we can divide. The right side was agian 1 so after dividing we get our answer $\frac{dy}{dx}=\frac{1}{y\cos(y)+\sin(y)}$. Since we do not know what $\sin(y)$ or $y\cos(y)$ are we cannot go any further and must leave our answer in this form.

