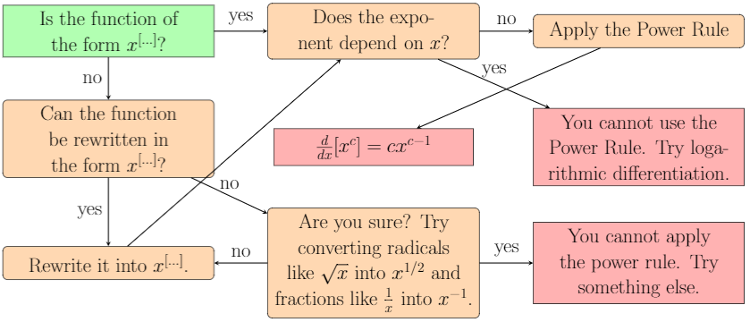
What is the power rule?
When the function is of the form $x^c$ for some constant $c$ then the derivative is $cx^{c-1}$.When do we use the power rule?
It should be obvious that when $x$ is raised to a positive integer power that the power rule applies. But the power rule applies for any real exponent. Fractions, decimals, constants, and even negative numbers are acceptable exponents to apply the power rule. Just make sure that the base is exactly $x$ (or whatever variable you are differentiating with respect to) and that there is nothing else happening in the function other than raising $x$ to a constant power.
Some functions are not obviously power functions. Any radical should be converted to a fractional exponent. And any power of $x$ in the denominator should be converted to a negative exponent so that the denominator is just 1. For example, $\sqrt{x}$ and $\frac{1}{x^2}$ are power functions and the power rule should be applied to $x^{1/2}$ and $x^{-2}$ respectively.

