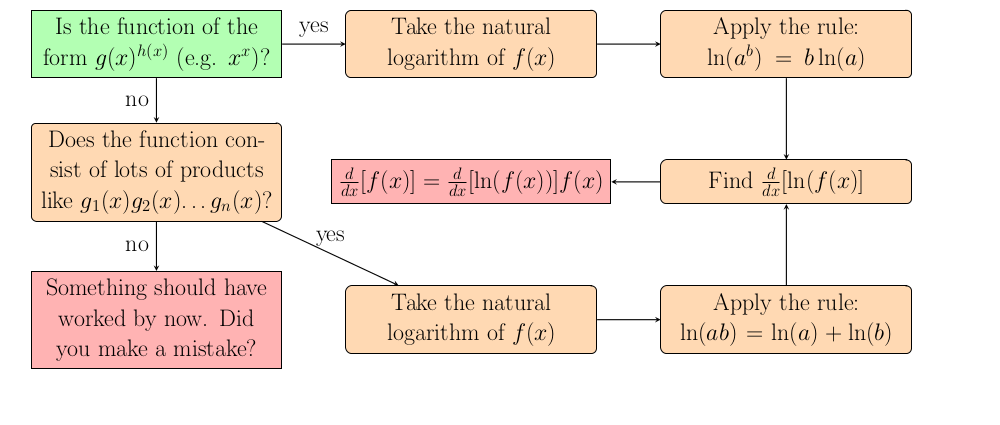
When is logarithmic differentiation used?
Only use logarithmic differentiation when taking the derivative without taking a logarithm seems impossible or would take many steps. One time when logarithms are unavoidable is when a function of $x$ is raised to an exponent that is also a function of $x$. The other time logarithms are used is when the function consists of the product of many functions of $x$. In this case it is possible to repeatedly apply the product rule, but logarithmic differentiation will be faster if there are several factors. Note that logarithmic differentiation is generally used on functions that do not have any logarithms involved.
What is logarithmic differentiation?
The first step is to take the natural logarithm of the function. The only reason logarithmic differentiation helps is because properties of logarithms can simplify the problem so the next step is to apply one of two properties of logarithms. Either bring the exponent inside the logarithm to the front or separate the factors into a sum of logarithms. Then this new function should be easier to differentiate so do that now using the sum or product rule. Then to end up with the derivative we want we multiply this derivative by the original function.


